Wpływ wielkości próbki na ocenę zdolności procesu (Cp, Cpk)

„Jak duża musi być próbka, aby ocenić zdolność procesu?” Ta kwestia nieustannie jest podnoszona przez uczestników szkoleń z SPC oraz MSA. Udzielenie odpowiedzi na to z pozoru proste pytanie wcale nie jest takie łatwe, zwłaszcza, że w przedstawionej formie nie jest ono do końca poprawne. 

Można by wręcz stwierdzić, że próbka brana do oceny zdolności procesu może być dowolnie mała, pod warunkiem, że jesteśmy w stanie zaakceptować dowolnie duży błąd tej oceny.

Podsumowując powyższe uwagi dochodzimy do właściwego sformułowania, które brzmi: Jak duża musi być próbka, aby dokonana na jej podstawie ocena zdolności była obarczona błędem, który mieści się w określonym przedziale. Na to pytanie można już odpowiedzieć. 

Poziom ufności

Zanim zaczniemy zagłębiać się w konkretne wyliczenia, musimy wyjaśnić kilka podstawowych pojęć. Pierwszym z nich jest tak zwany przedział ufności, w statystyce określany często za pomocą wyrażenia 1 – α. Bez wchodzenia w zawiłe definicje i wzory statystyczne możemy stwierdzić, że jest to akceptowane przez nas prawdopodobieństwo, że dany parametr mieści się w pewnym przedziale.

W praktyce statystycznej najczęściej posługuje się poziomami ufności o wartościach 0,9; 0,95 lub 0,99. Na przykład jeżeli powiemy, że nasze obliczenia są wykonane z poziomem ufności 0,95, oznacza to, że 95 przypadkach na 100 (w 95 procentach) mamy rację, natomiast w 5 przypadkach na 100 jesteśmy w błędzie.

Załóżmy, że wyznaczyliśmy współczynnik zdolności Cpk, który wyniósł 1,33. Jednocześnie przyjmujemy, że w obliczeniach zaakceptowaliśmy poziom ufności 1- α równy 0,95. Oznacza to, że informujemy wszem i wobec, że zakładamy iż rację będziemy mieli tylko w 95% przypadków. Takie podejście może wydawać się dziwne, ale w statystyce jest powszechnie przyjęte.

Przedział ufności

Od poziomu ufności już tylko krok do przedziału ufności. Otóż okazuje się, że oprócz podania „jakości” statystycznej naszego wyniku musimy jeszcze doprecyzować przedział, w którym rzeczywiście się on znajduje. Załóżmy jeszcze raz, że w obliczeniach uzyskaliśmy współczynnik zdolności Cpk równy dokładnie 1,33. Gdybyśmy chcieli się teraz zapytać, jakie jest prawdopodobieństwo, że proces ma dokładnie zdolność 1,33, uzyskalibyśmy wynik w okolicach zera, ponieważ zawsze rzeczywista wartość będzie odbiegała nieco w dół lub nieco w górę od założonej wartości. Musimy więc sformułować problem inaczej, zadając pytanie „Jak szeroki musi być przedział obejmujący uzyskany przez nas wynik (czyli np. Cpk=1,33), aby prawdopodobieństwo znalezienia się w tym przedziale było nie mniejsze niż założony poziom ufności”. Odpowiedzią na to pytanie jest właśnie przedział ufności.

Warto tu zastanowić się nad wzajemnym powiązaniem poziomu i przedziału ufności. Im wyższy poziom ufności, tym szerszy przedział ufności. Wyobraźmy sobie, że strzelamy do celu z łuku. Jeżeli chcemy wyznaczyć obszar tarczy, w który trafia 90% naszych strzał, wyznaczymy mniejszą powierzchnię niż w przypadku, gdybyśmy chcieli wyznaczyć obszar, w który trafia 99% strzał. Taka sama zależność występuje między poziomem ufności a przedziałem ufności.

Należy również podkreślić, że poziom ufności jest wartością względną (bo procentową) natomiast przedział ufności, to wartość bezwzględna. Jeżeli na przykład tniemy kawałki drewna na odcinki o długości 100 cm, to przy poziomie ufności 0,95 będziemy szukali takiego przedziału rzeczywistych długości naciętych kawałków drewna, który obejmie 95% tych kawałków. Oczywiście przedział ten będzie wyrażony w centymetrach.

Wpływ wielkości próbki na szerokość przedziału ufności

Jak łatwo się domyślić, z punktu widzenia jakości danych statystycznych interesuje nas jak najwęższy przedział ufności. Szeroki przedział ufności oznacza dużą niepewność wyniku, a to zawsze jest niepożądane. Przedział ufności możemy zawężać obniżając poziom ufności, ale to z kolei oznacza, że zgadzamy się na mniejszą procentową trafność oceny. Czy istnieje więc inny czynnik, który wpływa na szerokość przedziału ufności bez ingerencji w poziom ufności? Tym czynnikiem jest wielkość próbki.

Intuicyjnie wyczuwamy, że wraz ze wzrostem liczności próbki przedział ufności będzie się zawężał. By to potwierdzić, wystarczy przeprowadzić prosty eksperyment myślowy, Załóżmy, że pytamy się 3 przypadkowych osób, czy mają psa. Prawdopodobieństwo, że natkniemy się na 2 a nawet 3 wielbicieli tego zwierzaka, jest stosunkowo duże. Możemy więc na podstawie takiego badania wysnuć ryzykowną konkluzję, że 66% lub 100% ludzi posiada psy. Takie wnioski są obarczone ogromnym błędem. Gdybyśmy jednak to samo pytanie zadali nie trzem a trzystu osobom, prawdopodobieństwo, że uzyskany wynik będzie zbliżony do rzeczywistości (czyli do proporcji występującej w całej populacji) jest znacznie większe. To samo możemy wyrazić posługując się pojęciem przedziału ufności – dla danego poziomu ufności wraz ze wzrostem badanej próbki następuje zawężanie przedziału ufności.

Przedział ufności w współczynniki zdolności procesu

Jak powyższe uwagi przekładają się na problem wielkości próbki branej do oceny zdolności procesu? Odpowiedzi na to pytanie udziela poniższy wykres.

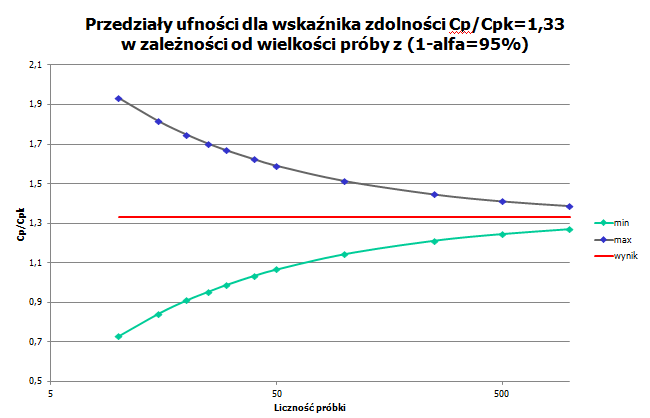
Wykres przedstawia sytuację, w której zaobserwowana (a więc nie rzeczywista, tylko taka, jaka wyszła z pomiarów!) wartość współczynnika zdolności wyniosła 1,33. Widoczne u góry i u dołu hiperboloidalne krzywe zakreślają granice przedziału ufności, w którym z prawdopodobieństwem 95% (bo przyjęto poziom ufności 0,95) znajduje się „prawdziwy” wynik.

Jak widać, im mniejsza próbka, tym szerszy przedział ufności. Na przykład dla próbki liczącej 50 sztuk rzeczywista zdolność procesu może wahać się w przedziale od 1 (wartość na dolnej krzywej dla próbki o liczności 50) do 1,6 (wartość na górnej krzywej). Innymi słowy, chociaż zdolność wykazana w obliczeniach wyszła 1,33, proces równie dobrze może mieć zdolność na poziomie 1 (a więc poniżej oczekiwań klienta) lub 1,67 (a więc znacznie powyżej naszych potrzeb).

Z tak szerokiego przedziału ufności wynikają dalsze konsekwencje. Otóż może się okazać, że jeżeli za jakiś czas dokonamy kolejnych 50 pomiarów i stosując ten sam algorytm spróbujemy z nich jeszcze raz wyliczyć współczynnik zdolności, to uzyskany wynik może znacząco odbiegać od poprzedniego mimo, że w procesie nie zaszły żadne zmiany. Może to z kolei prowadzić do błędnych wniosków o niestabilności procesu (no bo przecież współczynnik zdolności „skacze”), podczas gdy problem tkwi w małej liczności próbki.

Wnioski

Czas więc na końcowe konkluzje. Najważniejszym stwierdzeniem jest, że zbyt mała próbka brana do oceny zdolności procesu może prowadzić do dużego błędu w tej ocenie. Stąd też przemysł motoryzacyjny zaleca wyznaczanie współczynników zdolności Cp, Cpk, Pp i Ppk na bazie próbki obejmującej co najmniej 100 jednostkowych pomiarów (spotyka się również wymagania obniżone do 75 jak i podwyższone do 125). Można więc powiedzieć, że przyjmując wartość 100 jako minimalną wielkość próbki klienci niejako narzucają dopuszczalną szerokość przedziału ufności, a mówiąc jeszcze inaczej dopuszczalny błąd, z jakim wyznaczamy te współczynniki. Tym samym, jeżeli organizacja podejmuje decyzję o wyznaczania współczynnika zdolności na podstawie mniejszej próbki, automatycznie aprobuje (niestety często bez zgody klienta) zwiększone ryzyko błędności tej oceny.

Na zakończenie pozostaje jedynie wyrazić nadzieję, że po lekturze tego artykułu dla każdego stanie się oczywiste, że pytanie „Jak duża musi być próbka, aby ocenić zdolność procesu?” po prostu nie ma sensu.